Exercice de Multiplication x10 x100 x1000 : Calcul mental / en ligne / posé CE1 CE2 CM1 CM2

Trouvez sur cette page un exercice idéal à afficher en classe pour travailler la règle des zéros. Je faisais ça de mon côté (surtout car je trouvais cela intéressant pour entraîner les élèves rapidement lors d’un rituel de calcul mental) et je me suis dit que le mettre à disposition de tous sur Bureau des Profs était une bonne idée.

Attention l’outil n’est pas parfait (notamment la décomposition automatique) car je n’ai pas eu beaucoup de le temps de le développer. Mais comme il est fonctionnel je vous laisse en profiter. N’hésitez pas à me contacter si des fonctionnalités sont cassées via l’onglet contact.

Règle des 0 : Entraînement en ligne

Sélectionnez un multiplicateur et générez un calcul, puis cliquez sur « Afficher le résultat » pour voir la réponse.

N1 x N2 = ?

Outil en ligne : les 4 opérations à travailler notamment en calcul mental https://bureaudesprofs.com/4-operations

La règle des zéros en mathématiques : comment l’enseigner efficacement au primaire ?

Attention, on va commencer par casser un mythe : la fameuse règle « pour multiplier par 10, on ajoute un zéro » est à PROSCRIRE (oui, oui, vous avez bien lu !). Pourquoi ? Parce que cette règle devient un véritable cauchemar quand on arrive aux nombres décimaux.

1. Le cas du multiplicateur avec des zéros à la fin

Prenons un exemple tout simple (parce que les exemples, c’est la vie !) : Quand vous multipliez 234 × 300, au lieu de vous arracher les cheveux, faites simplement :

• La multiplication 234 × 3 (beaucoup plus simple, n’est-ce pas ?)
• Puis ajoutez les deux zéros du 300 au résultat

Petite parenthèse : cette méthode fonctionne parfaitement, mais il faut bien comprendre POURQUOI elle marche (sinon, c’est comme apprendre une recette de cuisine sans savoir à quoi servent les ingrédients).

2. Comment fonctionne la règle des zéros ? Quelle leçon donner aux élèves ?

Pour comprendre la multiplication par 10 ou 100, il faut décomposer le processus (un peu comme un détective qui résout une enquête) :

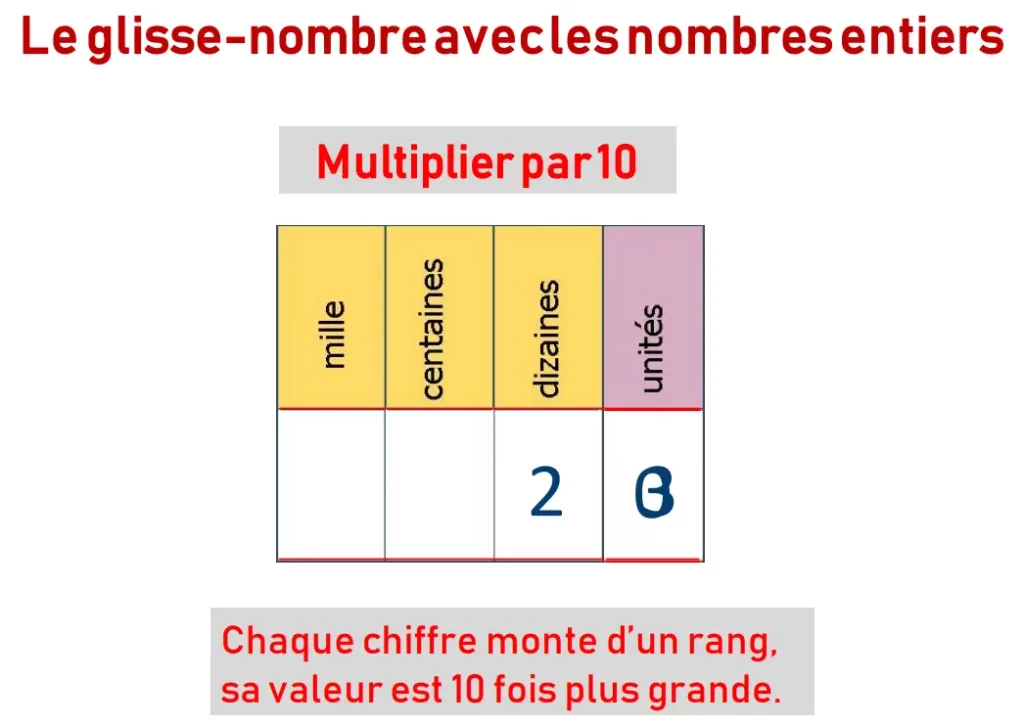
La décomposition du nombre Prenons 23 × 10 :

• 23, c’est 2 dizaines et 3 unités (première étape de notre enquête !)
• Quand on multiplie par 10, chaque chiffre devient 10 fois plus grand (à retenir donc)
• Les chiffres se déplacent d’un rang vers la gauche dans le tableau de numération
• Et voilà qu’apparaît notre ami le zéro dans la colonne des unités !

Le tableau de numération est votre meilleur allié pour travailler la règle des 0 de mon point de vue. Un petit glisse-nombre en cycle 2 et ça sera plus visible et compréhensible pour eux.

Les pièges à éviter (parce qu’on apprend tous de nos erreurs)

• Ne pas donner la règle toute faite (faites leur observer plusieurs calculs et résultats)
• Éviter les raccourcis du type « ajoute un zéro » (problématique pour les nombres décimaux)
• Ne pas négliger la compréhension du système décimal de position (la base)

Pour conclure, rappelez-vous que la règle des zéros, ce n’est pas une formule magique à appliquer aveuglément. C’est une compréhension profonde de notre système de numération (oui, je sais, ça fait un peu pompeux dit comme ça, mais c’est vrai !).

Utilisez la décomposition pour travailler la règle des zéros

Si vous cherchez LA méthode qui débloque vraiment la compréhension (et croyez-moi, j’ai testé pas mal de choses !), c’est bien la décomposition des nombres. Elle permet d’utiliser les propriétés de la multiplication de façon naturelle et logique.

Prenons un exemple concret : 345 × 20

L’associativité nous permet de faire des merveilles :

• 20 se décompose en 2 × 10
• Donc 345 × 20 devient 345 × (2 × 10)
• Ce qui nous donne (345 × 2) × 10
• Et là, magie : on fait d’abord 345 × 2 = 690, puis × 10

La distributivité n’est pas en reste (et c’est un SUPER outil) :

• 345 se décompose en 300 + 40 + 5
• Notre multiplication devient (300 × 20) + (40 × 20) + (5 × 20)
• Soit 6000 + 800 + 100 = 6900

Pour aider les élèves à visualiser tout ça (parce que les maths, c’est aussi visuel !), j’utilise un système de couleurs différentes pour chaque étape de la décomposition. C’est fou comme un peu de couleur peut rendre les maths plus sympas ! 😀

Source des images : https://edu1d.ac-toulouse.fr/politique-educative-31/ien31-tournefeuille/files/2020/10/Temps-1-Enseigner-les-differentes-strategies-de-calcul-au-cycle-2.pdf